- TOP
- 技術情報
技術情報
Technical Information
負の温度特性をもった温度センサの王様
サーミスタとは、ファインセラミックス半導体の感熱素子
サーミスタとは、熱に敏感な抵抗体ということで、温度の変化につれてその抵抗値がきわめて大きく変化する半導体です。
一般の物質は温度が上がると抵抗値もわずかに上がります。芝浦電子が製造するNTCサーミスタは、抵抗値が大きく下がっていきます。以下の説明はNTCサーミスタに限ったものとします。
サーミスタは、Mn、Ni、Coを主体とする遷移金属酸化物の数種を原料とし、焼結されたファインセラミックス半導体の感熱素子です。
使用温度範囲が−50〜+500℃と日常温度コントロールを必要とする全範囲をカバーしており、小形で安定かつ高感度のため、家電機器や産業機器に温度センサや温度補償用として大量に使われています。
NTCサーミスタ電気伝導性の解説
一般的に金属は温度が上がると抵抗値も上昇することが知られています。
金属は自由電子をたくさん持っています。“電気の流れやすさ”は“自由電子の進みやすさ”に等しく、温度が高くなると金属原子の振動が激しくなり、自由電子の進行を邪魔するために電気は流れにくくなり、抵抗値が上昇するという現象に顕れてきます。
これに対してNTCサーミスタは自由電子をあまり持っていません。
このため金属と比べて室温付近では電気を流しにくい性質があります。
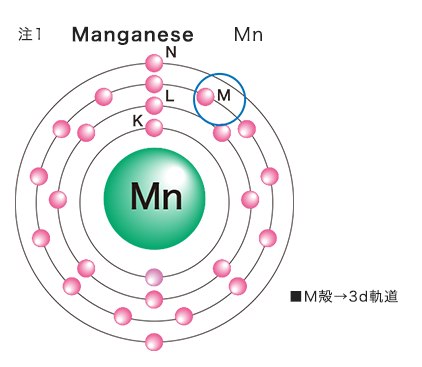
サーミスタは一般的にMnの3d電子の移動が関与していることが知られています。 ※注1
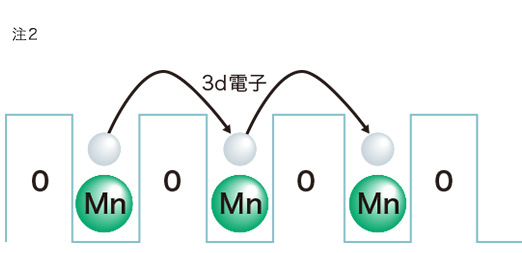
NTCサーミスタの電気伝導は「自由電子とホール」、2つのキャリアの動きにより生じています。電子(Mn
3d電子)がホールに入ったら直ぐに次のホールへ移動する。この運動を繰り返すことで電気の流れを生み出しています。これをホッピング電導と呼んでいます。
※注2
温度が低いときは自由電子の数が少なく動きも緩慢であるため、電気は流れにくくなり抵抗値は高くなります。温度の上昇とともにキャリアの数が増え、電子の移動(ホッピング)も熱振動により助けられるため、電気が流れやすくなります。
このような金属とは異なる電気伝導により、NTCサーミスタは温度が上がると抵抗値が減少する特徴を持ち、組み合わせる材料と混合比率の違いによって様々な特性を生み出しています。
サーミスタの物理的性質
4定数で決まるサーミスタ特性
サーミスタの特性は、基本的には抵抗値 R、B定数 B、熱放散定数 δ、熱時定数
τの4定数で表されます。
これらの4定数を基本として、「電流-電圧特性」「抵抗温度係数」が補助的に用いられることがあります。
各性質の詳細はこちら
サーミスタの抵抗値はJIS C 5602に以下のように規定されています。「測定の総合誤差に比べ、自己加熱による抵抗変化が無視できるような十分低い消費電力において、規定温度で測定した場合のサーミスタ素子の直流抵抗値」
芝浦電子では測定電流値の標準化を行い、大変精度の高い自社開発の恒温槽を使用してサーミスタの抵抗値を測定しています。芝浦電子で製造しているのは、NTCサーミスタという「負の温度係数を有するサーミスタ」であり、温度が上昇すると抵抗値が減少する特徴を持っています。サーミスタの抵抗値Rと絶対温度Tとの関係は、近似的に式で表すことができます。
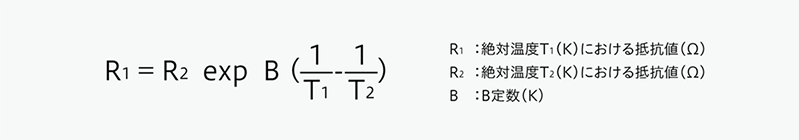
様々な特性のサーミスタから適切な物を選択する目安として、使用温度の範囲で抵抗値の幅が100Ω~100kΩであることが回路設計上望ましいとされています。
芝浦電子の豊富な特性ラインアップの中から、使用温度範囲に応じたサーミスタをお選びください。
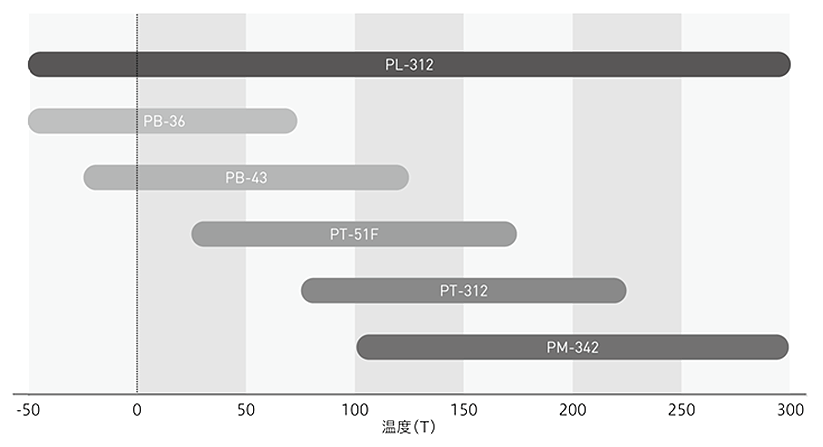
抵抗値は、サーミスタチップのサイズを変えることで調整することができます。芝浦電子では、標準品のほか、お客様が希望される特性へのカスタマイズにも対応しています。
B定数は温度変化に対するサーミスタの感度(抵抗値の変化の割合)を表す物性値です。
変化の割合はグラフの傾きで表すこともできます。この傾きが大きいほどB定数が大きく温度変化に対する感度が高いということができます。
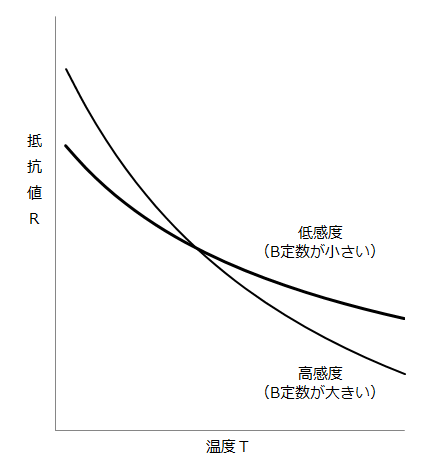
B定数は、規定した2温度間の抵抗値変化から計算で求めます。
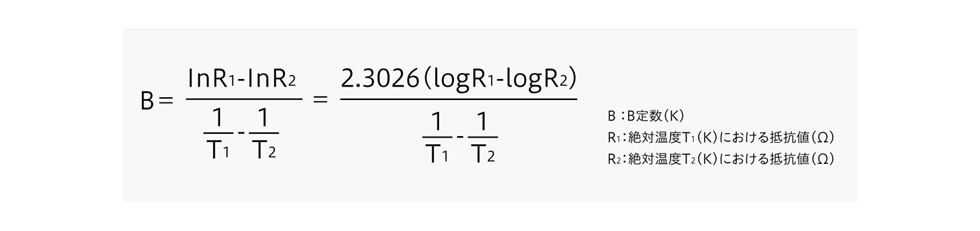
B定数はサーミスタチップの材料組成により決まるため、抵抗値と異なり、サーミスタチップのサイズの変更では変えることができません。
また、一般的にB定数の大きいサーミスタは抵抗値が高くなるという特徴があるため、抵抗値とB定数の組み合わせを自由に選ぶことはできません。
たとえば、非常に高い抵抗値で、極めて低いB定数のサーミスタを作ることは困難です。
芝浦電子では、数多くの抵抗値とB定数の組み合わせの製品を有しており、カタログや当サイトに掲載しているのはそのうちの一部です。
特殊なB定数のサーミスタのご相談もお受けしています。
B0/100のB定数計算の一例を示します。

熱放散定数δとは、静止空気雰囲気においてサーミスタ自身が通電による自己加熱で1℃温度上昇するために必要な電力(mW/℃)のことです。
周囲温度Taにおいて電力Wを印加したとき、自己加熱によって最終的にサーミスタの温度がTになったとすれば、以下の関係が成立します。

熱放散定数相当の電力を印加するとサーミスタの温度が+1℃上昇するため、これは周囲温度との誤差となって計測データに反映されてしまいます。
そのため、測定に問題のない範囲の自己加熱に抑えるような印加電力となる回路設計をする必要があります。
また、熱放散定数δは「自己加熱」と「放熱」のバランスで決まるため、サーミスタの周囲の状況で大きく変わります。
熱伝導率の高い素材でサーミスタを囲むことで熱の放散が促されると、熱放散定数δは大きくなります。
逆に熱がこもるような構造の場合、熱放散定数δが小さくなることもあるため、アセンブリに際しての材料選択は大変重要です。
アセンブリ後には使用する環境(空気、水、オイル、熱板接触etc.)において熱放散定数δを計測して、実使用に即したデータを取得する必要があります。
自動入力計算フォーム
ご利用条件を入力いただくことで、熱放散定数の算出が可能です。
【ご注意】
算出された結果は、当社の製品の性能を保証するものではございませんのでご注意ください。
※ W÷(T-Ta) か (I×I×R)÷(T-Ta) で算出が可能です。
5項目すべてが必須ではありません。
W、T、Taの3項目 か I、R、T、Taの4項目 の入力で算出が可能です。
熱時定数は温度変化に対する応答性の度合いを表した定数です。
サーミスタの周囲温度をT1からT2に変化させたとき、経過時間t
(sec.)とサーミスタ温度Tとのあいだには次の関係が成立しています。
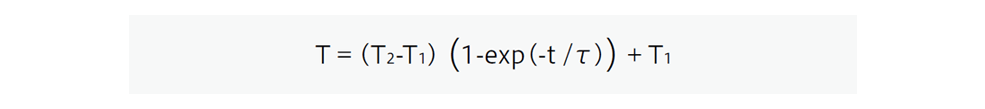
関係式中のτ (タウ、単位:sec.)が熱時定数です。
ここで、t=τ(タウ)とすると以下のように表すことができます。
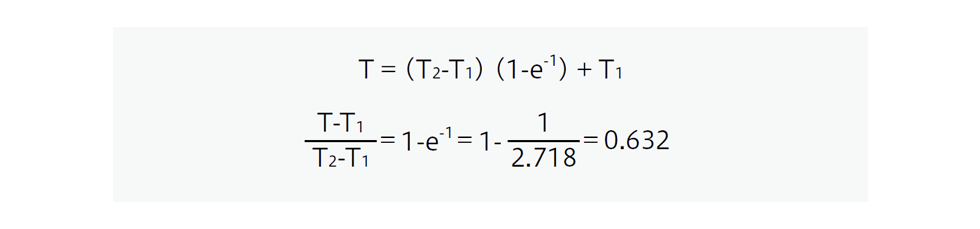
このことからサーミスタの温度が、初期の温度差の63.2%変化するまでの時間を熱時定数τ
(sec.)と定義しています。
熱時定数で定義された時間では、サーミスタの温度は周囲温度までは達していません。
τ
(sec.)をn倍したときの温度変化率は以下の通りで、熱時定数の約7倍でサーミスタの温度は周囲温度に到達します。
τ= 63.2% 2τ = 86.5% 3τ = 95.0% ・・・・ 7τ ≒ 100%
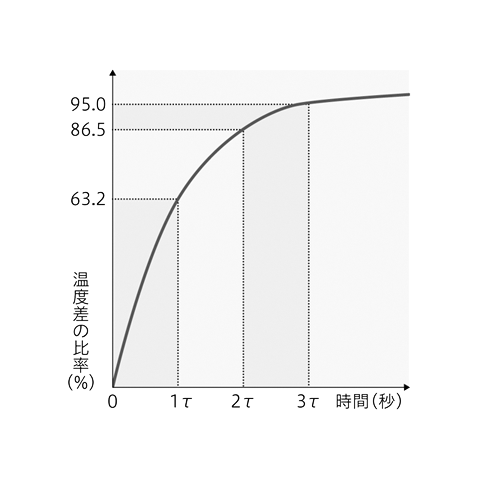
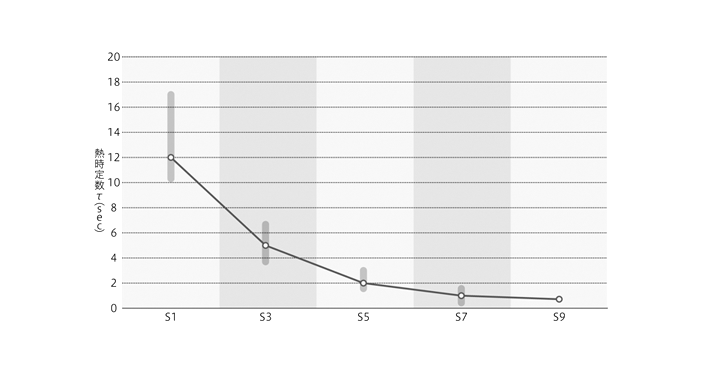
サーミスタの体積が小さくなるほど応答速度が速くなるため、小型のサーミスタの方が熱時定数τは小さくなります。
また、サーミスタのアセンブリによっても大きく変わるため、使用環境を充分考慮したうえで、熱伝導率のよい材料を選定することも必要です。
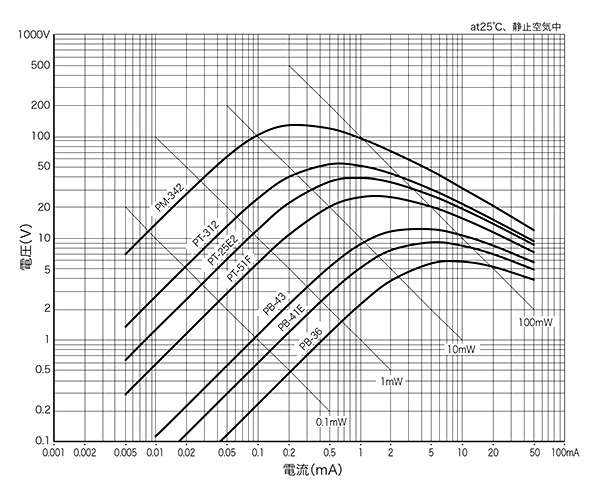
電流-電圧特性(I-V特性)とは、サーミスタに電流を流した際の電圧変化をグラフに表したものです。
NTCサーミスタの電流-電圧特性(I-V特性)の特徴は、電流値が大きくなるに従って直線的に電圧値が大きくなります。
しかし、ある電流値をピークにして電圧は降下を始めます。
電流を流すとサーミスタは自己加熱し、電流量の増加とともに発熱量も大きくなっていきます。
発熱量が小さいあいだは、発熱量に対してリード線からの放熱や、サーミスタ表面からの輻射による放熱量が大きいため、サーミスタ自身の温度が変化せず、抵抗値は変動しません。オームの法則に従って、電流と電圧は比例関係にあります。
しかし、発熱量が放熱量よりも大きくなるとサーミスタ自身の温度が上昇し、抵抗値が減少し、電流と電圧は比例関係ではなくなります。このため、ある点を境にして徐々に電圧値は低くなっていきます。
サーミスタ素子の電流-電圧特性を示します。通常はサーミスタの自己加熱が抵抗値変化に及ぼす影響が小さい、グラフが直線を示している領域で使用します。
また、グラフの頂点が示している電圧を超える印加電圧で使用した場合は、サーミスタが抵抗値減少と自己加熱を繰り返す「暴走モード」に入り、短時間で赤熱して破損する可能性があるため、特に注意が必要です。
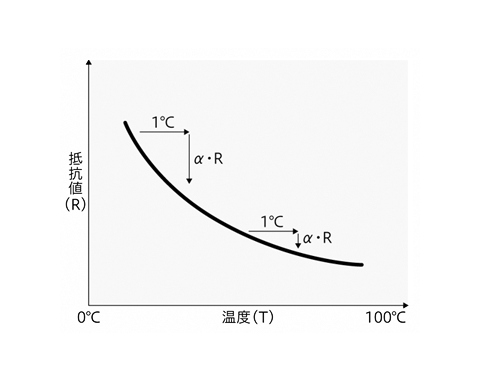
抵抗温度係数とは、サーミスタの抵抗が温度1℃あたりどのくらいの割合で変化するかを表す係数です。記号はαで、単位は%/℃
です。
抵抗温度係数αは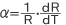 で表されます。ここで、サーミスタの抵抗値Rと絶対温度Tとの関係式(「抵抗値」の項目を参照)を温度Tについて微分し、αを求める式に代入すると、次式のようになります。
で表されます。ここで、サーミスタの抵抗値Rと絶対温度Tとの関係式(「抵抗値」の項目を参照)を温度Tについて微分し、αを求める式に代入すると、次式のようになります。
温度係数αの符号が(ー)であることは、サーミスタの抵抗が温度の上昇とともに減少することを示すもので、B定数を3400Kとして20℃付近の温度係数を求めると
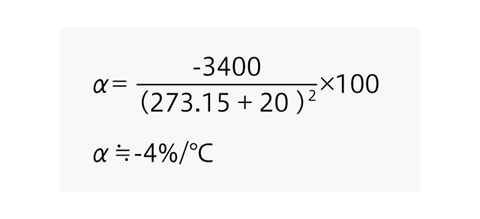
温度係数α≒-4%/℃ということになります。
一般に金属や合金は、温度の上昇につれて抵抗値が上昇し、その温度係数は、1℃の温度変化に対して0.4%(金)、0.39%(白金)、大きいものでも0.66%(鉄)、0.67%(ニッケル)であり、サーミスタが約 −4%ということは、僅かな温度変化に対して大きく抵抗が変化することです。このことから、サーミスタは精密温度計測や微小温度差コントロールに適した温度センサであるといえます。
サーミスタ素子の絶縁抵抗はリード線-ガラス間における絶縁性のことをいいます。
十分な絶縁性があることは、耐久性能を確保するうえで大変重要です。
芝浦電子ではPSB-N形、KG形を除く全製品の絶縁抵抗を全数測定しています。
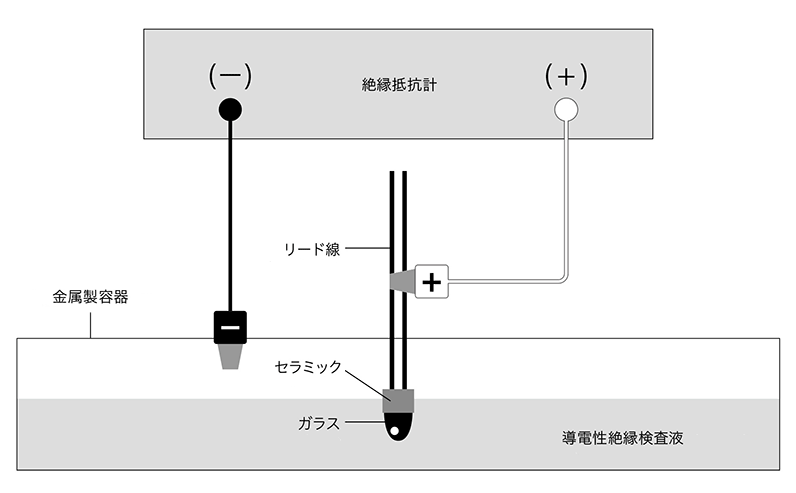
絶縁抵抗の測定方法を下図に示します。
金属製の容器に導電性の絶縁検査液を充填して、サーミスタのガラス部分(NS形はガラスとセラミックの境界部分まで)を浸漬します。
絶縁抵抗計の陽極(+)をサーミスタリード線に接続し、絶縁抵抗計の陰極(-)を金属容器に接続して、リード線-ガラス間における絶縁抵抗を測定します。